1 Prof. Jones: There’s a felucca owner. Let’s negotiate passage.
2 Monty: Greetings! We’re going to Alexandria. Can you get us there before the next train, in six days?
3 Felucca owner: To tell you the truth, I’m not sure whether it will take six days or only five.
4 Felucca owner: You’ve got to ask yourself one question: Do you felucca, punk?

A felucca is the traditional wooden sailing boat used along the Nile River as well as in nearby areas in the eastern Mediterranean Sea and Red Sea. Feluccas use a distinctive triangular lateen rigged sail (also sometimes used by the dhows of the Indian Ocean).

After coming up with the idea for this comic, I had to^[1] check that it is in fact feasible to sail from Al Balyana to Alexandria in under six days. It simply wouldn't do to make this joke and then have someone point out that it's impossible to sail to Alexandria faster than just waiting for the next train.

Firstly, how far is it from Al Balyana to Alexandria? Unfortunately, Google Maps doesn't give travel times or distances for travel by river, but it does offer this driving route, which comes to a distance of 749 km. (As well as this walking route, which clocks in at a relatively leisurely 691 km.) The road route doesn't follow the river, but has some deviations which to my eye very roughly match the meanderings of the Nile, so let's assume a rough distance of 750 km from Al Balyana to Alexandria by river.

Secondly, how fast does a felucca typically sail? Good question! Unfortunately I couldn't find any completely straightforward answers to this online. The most informative was this reddit thread, asking essentially the same question (albeit with an amusing typo), but failing to give a definitive answer.

One important reference that came up is the hull speed of a water vessel. This is a speed defined as being that at which the length of the vessel's bow wave is equal to the length of the vessel's waterline (the length of the vessel measured at the horizontal line defined by the surface of still water as the vessel floats). The bow wave of a boat is generated by the prow of the vessel pushing through the water, and because it is forced by the boat it necessarily has a wave speed equal to the speed of the boat. Fluid dynamics tells us that the wavelength of a water surface wave is proportional to the square of its velocity:

wavelength = K × (velocity)²

So:

bow wave velocity = √(wavelength / K)

Setting the wavelength equal to the vessel's waterline length gives:

hull speed (by definition) = bow wave velocity (when wavelength = waterline length) = √(waterline length / K)

hull speed = k √(waterline length)

where k = 1/√K is just another constant. This constant k is typically given as 1.34 when the waterline is measured in feet and the vessel speed in knots. This corresponds to 1.25 if the waterline length is in metres and the speed in metres per second.

Now, all we've done so far is define what the hull speed of a water vessel is. The actual speed of a boat also depends critically on how much power is being applied to propel it forwards, whether that be by means of an engine, a sail, or rowing (or indeed quanting, or being towed by draft animals). Simply put, the more power, the faster the vessel goes. Where the hull speed comes in is in figuring out how much resistance to motion the water offers. At low speeds, when the bow wave length is very short compared to the vessel's waterline length, the water resistance is fairly constant.

To figure out the relationship between motive power and water vessel speed, I tried a quick Google search, but didn't turn up an explicit equation, so I turned to one of the best resources available for calculating this sort of thing. Yes, you guessed it: GURPS Vehicles.^[2]

Page 131 of this roleplaying game sourcebook has this formula:

top water speed = 6 × ∛[(aquatic motive thrust) / (hydrodynamic drag)] miles per hour

where

hydrodynamic drag = ∛(loaded weight - contragravity lift)² / (hydrodynamic lines)

where (hydrodynamic lines) is a constant ranging from 1 for unstreamlined (e.g. a log) to 10 for average boat lines to 20 for very fine streamlining, plus 10% for a trimaran or 20% for a catamaran.^[3]

So, I'm willing to believe that—essentially—the top speed of a surface water vessel is proportional to the cube root of the thrust. But I still wanted to check if such a relationship can be found elsewhere. The best I could find was this (public domain) graph of power versus speed for a displacement hull from Wikipedia's page on Wave-making resistance:

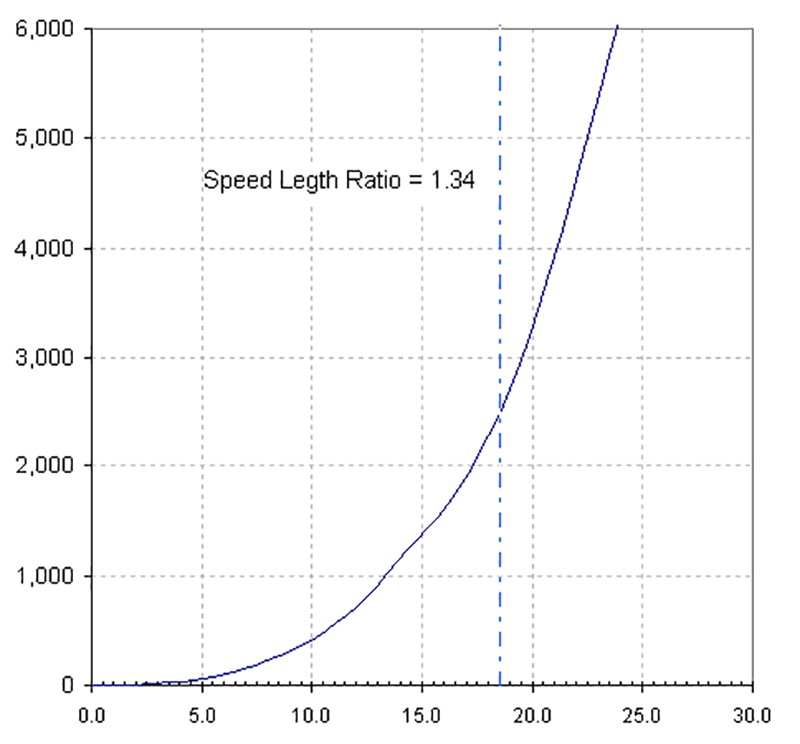
A quick and dirty measurement of points on the curve, plugged into a spreadsheet, then taking logarithms and plotting to find the slope, gives a value of around 2.7-2.9 for the power law exponent. This is of course a bit rough, but is within spitting distance of a cubic relationship, which gives me more confidence that GURPS Vehicles is correct to at least a first order approximation. Good.

Now, the hull speed comes about as a concept because when the boat is going fast enough to create a bow wave whose wavelength begins to approach the length of the waterline, you start to get some additional drag effects. Importantly, if the bow wave wavelength grows to 2/3 the waterline length, then the bow is sitting on the crest of the bow wave, while the stern of the boat is 1.5 wavelengths behind, in the next following trough. This adds turbulence because the stern of the boat also produces a wave system, and being in the bow wave trough causes constructive interference, increasing the energy lost into the water. If the boat powers through this up to the hull speed, the bow wave wavelength now equals the waterline length, and the bow and stern both sit on a wave crest. As boat speed increases, this is the final efficient mode for propelling a simple displacement hull (as opposed to a hydrofoil), and the amount of power required to go any faster now climbs steeply.

But if you simply apply MOAR POWER, you can continue to make your boat go faster, although it gets progressively less efficient in the amount of power you need to apply for an incremental speed gain. Eventually the bow wave wavelength approaches 1.5 times the waterline length. Now the bow is sitting on the bow wave crest, while the stern is sitting down in the immediately following trough, which means that your boat is now essentially moving uphill along the water surface. As you might imagine, this makes it even more difficult to propel the boat, compared to along a nice flat water surface.

MOAR POWER!!! will break you through this regime, into the zone where the bow wave wavelength is significantly greater than the vessel's waterline length. Now the boat is what is known as planing across the water, and in this zone efficiency increases again.

This (public domain) image from the US Naval Academy Engineering 400 Class, Chapter 7. RESISTANCE AND POWERING OF SHIPS (pp. 7-17), as available in Wikimedia Commons, illustrates the principle:

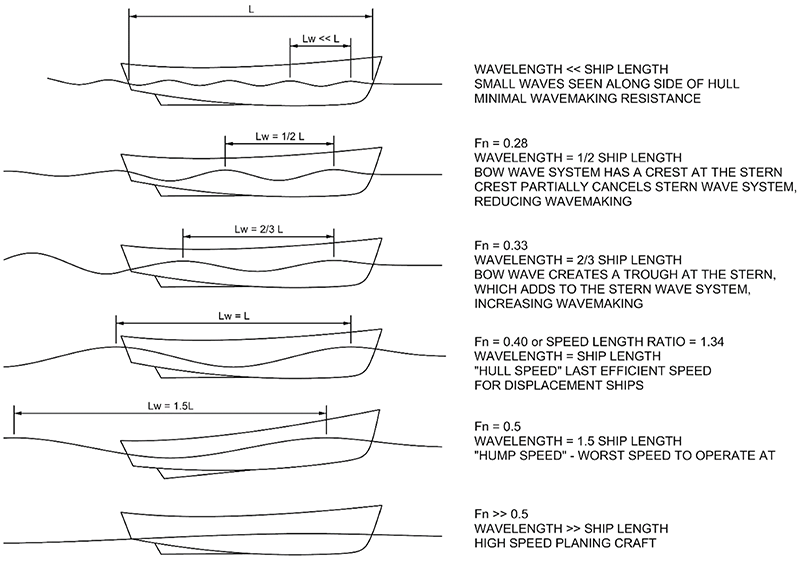
So, in short, the hull speed is not a maximum theoretical speed for a boat, but rather a speed around which it becomes very inefficient in terms of its power to speed ratio. Well above the hull speed, that efficiency returns. But for a standard displacement hulled sailing vessel, gaining enough power to break through the hull speed regime is always going to be difficult at best. Modern racing yachts and sailing dinghies can be designed to facilitate planing, but traditional sail-powered vessels such as feluccas are essentially limited to around 2/3× to 1× their hull speed as a maximum speed.

So what is the hull speed of a felucca? This first hand account says Nile feluccas range from about 15 to 30 feet in length. That gives them a hull speed of from 5.2 to 7.3 knots, or 9.6 to 13.5 km/h. If we assume that the winds are good and our felucca can make top speed, that gives us a total sailing time of 55-78 hours to cover the distance from Al Balyana to Alexandria, depending on the length of the felucca. So if we sail 10-13 hours a day, you can indeed make the trip in 6 days! If the owner only pulls to shore to sleep for 8 hours and sails for a full 16 each day, you can make the distance in 6 days at the relatively leisurely speed of just 7.8 km/h (or 4.2 knots), which should be doable.

Moreover, these are the theoretical speeds of a felucca relative to the water. The Nile flows downstream, from Al Balyana towards Alexandria. Even just holding onto a log, you would drift downstream and travel all the way eventually. So you can also add the speed of the water flow to the speed of the boat relative to the land. So a bit more research is required for our full answer.

Again, I didn't find any really good references for how fast the Nile flows. But I did find some stuff mentioning that the speed of rivers is highly variable, of course, depending on the terrain they are flowing over. But a reasonable speed for a large river is somewhere from 0-3 m/s, which adds anywhere from 0 to 10.8 km/h to our felucca speed. If we say the average speed over the length of the Nile between Al Balyana and Alexandria is 5 km/h, this makes our felucca speed anything up to 18.5 km/h, which can cover the distance in just 40.5 hours.^[4]

I really don't think a felucca would average a speed that high in practice, but even our previous high estimate of 78 hours sailing time makes it not unreasonable for our felucca owner here to state that he can get the Joneses to Alexandria in 5, maybe 6, days.

And so, the joke in this comic is valid.

---

[1] For some definition of "had to".

[2] For those not in the know, GURPS is a roleplaying game system, in the next tier of popularity down from the one occupied solely by the genre-defining behemoth that is Dungeons & Dragons. In contrast to the relatively high level of abstraction in Dungeons & Dragons, GURPS is known for being much more simulationist and realistic. Its sourcebooks are often cited for the depth and accuracy of their real world research, backed up by extensive bibliographies.^[2a]

GURPS Vehicles is without a doubt the pinnacle of this approach to gaming. It includes very detailed rules for designing almost any sort of vehicle you can imagine, from dugout canoe to faster-than-light spaceship, and then deriving all of the important statistics of the finished vehicle from the previous construction steps.^[2b] It is uncannily accurate. You can design a horse-drawn cart, a steam locomotive, a modern motor car, a helicopter, or a space shuttle using the known real world parameters for vehicle mass, engine power, and so on, and the included formulae within GURPS Vehicles will tell you the maximum speed, acceleration, cost, fuel consumption, etc, etc, of the vehicle, accurate to within maybe 10% of the real world values.

[2a] Also, I wrote a couple of them. And if you buy the PDFs I get royalties.

[2b] Obviously the performance of a faster-than-light engine has to be somewhat fictionalised. But you get the point.

[3] Yes, those formulae have cube roots in them. And you thought Dungeons & Dragons players were nerds.

[4] In fact, just drifting with your log 24 hours a day, you could make it to Alexandria in 6 and a quarter days, which is almost as fast as walking. In fact, in fact, the Joneses could have beaten the next train to Alexandria by walking.