

| Archive Blog Cast Forum RSS Books! Poll Results About Search Fan Art Podcast More Stuff Random |
|
Classic comic reruns every day
|
1 Jamie: Wait. I know what's happened. The waters of the Mnemosyne not only restore memory, they grant omniscience!
1 Adam: I know!
2 Jamie: We should test it to make absolutely sure.
2 Adam: I know!
3 Jamie: Is the Riemann hypothesis true or false?
3 Adam: It's true, but unprovable!
3 Jamie: I know!
4 Jamie: Wow! We should get the Millennium Prize for that!
4 Adam: I know! Alas, we won't.
4 Jamie: I know!
|
First (1) | Previous (1959) | Next (1961) || Latest Rerun (2858) |
Latest New (5380) First 5 | Previous 5 | Next 5 | Latest 5 Mythbusters theme: First | Previous | Next | Latest || First 5 | Previous 5 | Next 5 | Latest 5 This strip's permanent URL: http://www.irregularwebcomic.net/1960.html
Annotations off: turn on
Annotations on: turn off
|
The Millennium Prizes are a set of seven cash prizes of the value of US$1,000,000, offered by the Clay Mathematics Institute for solutions to outstanding unsolved problems in mathematics.
One of the seven problems, the Poincaré conjecture, has since been proven, but the author of the proof has not claimed the prize. The other six problems remain unsolved.
One of the unsolved problems is the Riemann hypothesis. This hypothesis is astoundingly simple to state:
All non-trivial zeroes of the Riemann zeta function have real part equal to 1/2.Astoundingly simple to state if you know the meanings of the following terms, that is:
I've touched on complex numbers a couple of times before: #1640 and #1845. It's time to dig a little deeper.
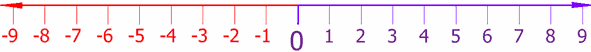 Let's start with the number line. This is a graphical representation of numbers, placed
along a single straight line, in order from smallest to largest. A fairly simple concept. But what numbers?
Let's start with the number line. This is a graphical representation of numbers, placed
along a single straight line, in order from smallest to largest. A fairly simple concept. But what numbers?
Our familiar counting numbers are all there. 1, 2, 3, etc. They extend to the right, equally spaced. if we have 2 apples and we get 3 more apples, we can figure out how many apples we have by starting at 2 and moving to the right 3 "spaces". We end up on 5, the number of apples we now have. Very handy.
If we go left just a little bit, we also have 0. If I have 2 apples and you take 2 away, I can figure out how many apples I have left by starting at 2 and moving 2 spaces to the left. I end up on 0. I have 0 apples left.
But we can go further than that. You can't take away more apples than I actually have, but what if we're talking about something like money? If I have 2 dollars and I owe you 3 dollars, how many dollars do I effectively have? Start at 2, go left 3 spaces, and I end up at a mysterious number labelled -1. I can't physically have -1 dollars, but you can interpret the minus sign on the number as meaning that I owe that amount of money, rather than have it free to spend on anything I want. What having "-1 dollar" means is that in order to clear all my debts, I need to earn 1 dollar.
Okay, that's slightly strange, but it actually works if you do your additions and subtractions on a number line that includes negative numbers, and it seems to be genuinely useful. In fact, this is how anyone dealing with accounts does arithmetic with money all the time. If you have money to spare, it's positive; if you have debts that you can't pay at the moment, it's negative.
We can also split apples (and dollars) into smaller pieces, like half an apple, or a hundredth of a dollar. These numbers fill in the gaps in between the whole numbers on our number line. There's a whole lot more I could say about these numbers, and what lies in between even them, but this is not the time or place for it.
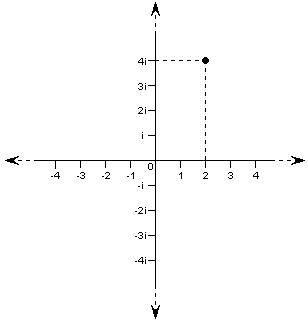 Instead, let's imagine that we add another number line to our first one. Where? At right angles! Going up and down!
Instead, let's imagine that we add another number line to our first one. Where? At right angles! Going up and down!
Now let's think how we can label this new number line. If we start at 0 and go one space right, we end up at 1. If we go one space left, we end up at -1. If we go one space up, we can't end up at 1 or -1, because we already know where they are; the number there has to be different. Let's call it i. And if we start at 0 and go one space down, we have to end up at another different number. Since it's in the opposite direction to i but the same distance from 0, it makes sense to call it -i.
We can keep going up or down. If we go up twice as far as i, that will be 2i; 3 times as far is 3i, and so on. Similarly, we can label -2i, -3i, etc. on the downward-pointing line.
But if we have two lines crossing at right angles, what about all the rest of the space around them? Are there numbers there too? Sure, why not! The diagram shows a point that is two spaces to the right of 0 and four spaces above 0. If it was on the horizontal line, we'd call it 2. If it was on the vertical line, we'd call it 4i. But it's out there... it's both 2 and 4i. So let's call it exactly that. That number indicated by the black dot is 2+4i.
But what does this addition add up to? Well it can't add up to a number on our regular horizontal number line, since it's above it. So it's definitely not 6, for example. And it can't add up to a number on our vertical line, since it's to the right of that line. So it's not 6i. In fact, it's not on either of our two number lines, so it must be a new, different type of number. Let's just call it 2+4i, since we know what that means, and not worry about the fact that there's a plus sign still in it.
Some of you no doubt know all of this already. The rest of you may be surprised to know that I'm not just making this up for the heck of it. These numbers, like 2i, -3i, and 2+4i, are actual numbers used in advanced mathematics and many fields based on it, such as physics, electronics, and computer science. They are called complex numbers.
You can do normal arithmetic with complex numbers, treating the i just like another number, as you would in algebra. For example:
As an aside, let's think about what complex numbers actually mean. Can I show you i apples? No, I can't. But neither can I show you -1 apples. But -1 is still a useful number to have, since it lets you do accounting. I can't show you -1 dollar either, but we can imagine what it means. Okay, so can I imagine what i dollars means? No, I can't. With dollars there's only two things you can do, gain them or lose them. That corresponds to moving right, or moving left. And since we start with 0, we can never get up or down off the normal number line.
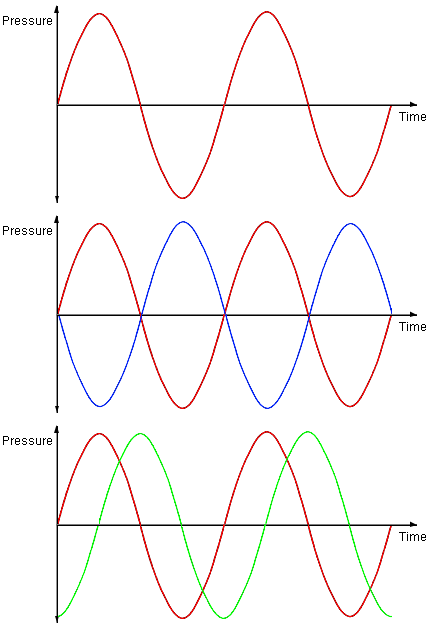 Let's think about something else. Sound waves.
Let's think about something else. Sound waves.
A sound wave is essentially ripples of changing pressure in the air (or in whatever else the sound is travelling through). If we measure the air pressure at our eardrum as a sound wave reaches us, we will see the pressure wobble up and down around the average air pressure. We can plot that like the red line on the graph here. That wobble in air pressure is what our ear detects as sound. Let's call this 1 unit of sound.
Now imagine another sound wave is coming into our ear. If it was exactly the same as the first sound wave, the same pressure variation and the same timing, then it would add up with the first wave. We would get 1 unit of sound, plus 1 unit of sound, equals 2 units of sound. So far, so good.
But now imagine the second sound wave is not lined up exactly like the first one in time. In fact, what if it is like the blue wave in the second diagram here, exactly the opposite of the first sound wave? At our ear, the red sound wave tries initially to raise the air pressure, but the blue sound wave tries to lower it by exactly the same amount. Wherever the red wave gives a certain increase in pressure, the blue wave gives a decrease of the same amount. And wherever the red waves tries to decrease the pressure, the blue wave is trying to increase it by the same amount! The end result is that the pressure at our ear doesn't change. And if there's no change in air pressure, we hear no sound.
This is how noise-cancelling headphones work. They detect the incoming sound waves from stuff you don't want to hear, like traffic, aircraft engines, or your little sister, and create the exact same sound wave, flipped upside down, in time for it to reach your ears at the same time. The fact that the blue wave cancels the red wave means that if the red wave is 1 unit of sound, the blue wave is effectively -1 unit of sound. Adding them together gives 0 units of sound.
Now imagine that the second sound wave is not lined up with the red wave, nor exactly the opposite either, but something like the green wave shown in the third diagram here. It turns out that if you add these two sound waves together, you don't get 2 units of sound, nor do you get 0 units of sound. You get something in between. In fact, for the example shown by the diagram, you end up with about 1.4 units of sound. Where did that number come from?
Let's think about what number of units of sound this green wave represents. We know the red wave is 1 unit of sound. The green wave is not -1 unit of sound, because it doesn't cancel the red one. But it's the same amount of pressure variation as the red wave, so it's 1 unit away from 0 units of sound. It's not right along the positive part of the number line, nor left along the negative part of the number line...
Some of you are thinking: "Is it up from the number line?"
Yes, it is. Relative to the red wave, the green wave is i units of sound. It's the same loudness as the red wave, but it's in a different direction. So the total units of sound reaching your ear is not 2, or 0, it is 1+i.
What does 1+i units of sound actually sound like? Well, how far away is it from 0? If you go 1 unit right and 1 unit up from 0, some simple geometry (Pythagoras' theorem) will tell you that you are the square root of 2 units from 0. The square root of 2 is approximately 1.414. That's how loud the total sound is to your ear.
This is how audio engineers actually do calculations involving sound waves. They use complex numbers, exactly like this. They use them because they work; they accurately describe how sound waves interact, and they give the right answers for questions like this. And it's not just audio engineers. Anywhere you get waves, complex numbers come in very useful to figure out what's going on. That includes anything to do with light, and almost anything to do with electricity. Think about how much of the stuff in our lives has to do with light, or electricity.
Seriously. Stop for a few seconds and think about it. Light. Electricity. What gadgets do you have that don't use one or both of those? That's how useful complex numbers are.
All right, we're now ready to tackle the Riemann hypothesis.
Complex numbers, as we've seen, have two parts: The distance you travel right or left of 0, and the distance you travel above or below 0. Left and right are our familiar everyday numbers. Mathematicians call these real numbers. The other part, moving up and down, is a bit out of the ordinary. When mathematicians first tried playing around with these numbers, they thought they were a bit strange, and they called them imaginary numbers. This should not be construed to imply that imaginary numbers don't exist. They're just called that because early mathematicians didn't know quite what to do with them yet. In many ways it is an unfortunate name, but we're stuck with it. We've already seen how useful they are.
So a complex number has a real part, and an imaginary part. In the number 2+4i, the real part is 2, and the imaginary part is 4i. Now we know what the real part of a number is, the first step to understanding the Riemann hypothesis!
The Riemann zeta function is a function of complex numbers. I've actually mentioned it before, and said that it was a long story for another annotation. Today is that annotation. :-)
If you recall from the annotation to #1640, a function is merely a rule for converting one number into another number. The Riemann zeta function takes any complex number you can think of, and converts it into another complex number. (Actually, there's a very small caveat there: The Riemann zeta function does not convert the number 1 into another number. But it does do every other complex number we care to name.) If you name a complex number with real part greater than 1 (let's call it z), the Riemann zeta function of that number is defined as follows:
Now, the Riemann zeta function equals zero whenever the number you feed in is any even negative real number; i.e. -2, -4, -6, etc. Where a function equals zero is called, strangely enough, a zero of the function. These zeroes, at -2, -4, -6, etc. are called the trivial zeroes of the Riemann zeta function. Which means that a non-trivial zero of the Riemann zeta function is a zero at any point in the complex numbers other than at -2, -4, -6, etc.
Recall the Riemann hypothesis:
All non-trivial zeroes of the Riemann zeta function have real part equal to 1/2.Besides the trivial zeroes, there are a bunch of other zeroes of the Riemann zeta function. All of them found so far have their real part exactly equal to 1/2. By "all of them found so far", I mean over ten trillion. That's right, ten trillion. (That's 1013, for those concerned about what trillions I'm using. Ten billion in the old British reckoning.)
You'd think that if there are well over a trillion known zeroes of this function, and they all have real part equal to 1/2, then it's probably true that every single non-trivial zero has real part equal to 1/2. Indeed, it may well be true. But the astonishing thing is that nobody has ever managed to prove it. And not for lack of trying, either. Many of the greatest mathematicians of the past 150 years have spent much of their lives trying to prove Riemann's hypothesis. This is one of the great unsolved problems in mathematics, and that is why if you can prove the Riemann hypothesis is true (or indeed prove that it is false!), you will win a Millennium Prize of US$1,000,000.
I am slightly disappointed.
|
LEGO® is a registered trademark of the LEGO Group of companies,
which does not sponsor, authorise, or endorse this site. This material is presented in accordance with the LEGO® Fair Play Guidelines. |