Irregular Webcomic! #3380

One aspect of physics which I've been a little reluctant to discuss here has been the physics of music. This is because music itself is a complex subject and one which I know comparatively little about, having never formally studied music theory or achieved even halting competence with any musical instrument until very recently. It is only really in the last year or so that I have started to learn anything about music theory.^[1]

Which is kind of odd, because music has extremely strong foundations in mathematics and physics, and there is a lot of fascinating stuff in the intersection of these fields. It's a bit odd as well that many (not all) musicians treat their field as simply an art form, without appreciating the physical and mathematical principles underlying it, or the amazing complexities that arise from the interactions of physics, mathematics, and the human aesthetics of creating and listening to music.

I never had the opportunities for musical tuition as a child, and I have often looked back on that fact with some regret. (It was circumstance, not any fault of my parents.) In later years I could only look on in envy as friends could pick up a guitar or noodle away on a piano or sing competently, while I could contribute nothing. But I loved listening to music.

While at university, one of my favourite physics lecturers released a book about the physics of music: Measured Tones. I bought it and asked Dr Johnston to sign my copy, and it sits on my bookshelf to this day. I understood physics, and I thought this book might be my gateway into understanding music. Unfortunately it wasn't, because although I understood the physics in the book, I could not understand the music theory in the book. There was a very basic level of music understanding that I was missing, and without it, talk about scales and modes and keys and minor and major chords and tunings and so on was all just a blank wall of incomprehension. I realised I knew literally nothing about how music worked.

My most basic question was "Why do the white keys on a piano have uneven frequency intervals between them? Shouldn't they all be the same interval?" The size of the difference - or, more technically, the ratio - between the sound frequencies of the notes C and D is called a tone. On a piano, there is a black key between the two white keys of C and D, giving a note halfway between them (called C-sharp, or D-flat). The interval from C to C-sharp is called a semitone, and then there's another semitone from C-sharp to D, giving the full tone from C to D. Okay so far.

Piano keyboards have an uneven arrangement of white keys with black keys in between.

Going from D to E we have a similar arrangement. In between is the black key which produces D-sharp (or E-flat), and there is a semitone from D to D-sharp, and another semitone from D-sharp to E, making a full tone from D to E. All good.

But when we go from E to F on a piano keyboard, there is no black key in between. E-sharp seems to be missing. What's more, the interval from E to F is not a tone, it is a semitone! What. The. Hell??

If you continue up the keyboard, from F to G is a tone, with the black key F-sharp in between. From G to A (the letters cycle around back to A after G) is a tone, with the black key G-sharp in between. from A to B is a tone, with the black key A-sharp in between. But from B to C is a semitone, with no black key in between. What in blazes is going on here?

If you play the notes of a scale in sequence on the white notes, C-D-E-F-G-A-B-C, it sounds nice, but the intervals are uneven: tone-tone-semitone-tone-tone-tone-semitone. Why are they uneven; why aren't the intervals all exactly the same? Surely, if there is any mathematical basis to music, the intervals must be the same, not jumping around in uneven steps. Or so I thought, and I could not understand why this obvious seeming principle was violated so flagrantly by how the piano and the notes were actually designed. And at the time I couldn't understand enough of the book to comprehend an answer.

I only discovered the answer within the last year. Basically, the scale of notes comes about because of human perception, and how our brains respond to sound.

Firstly, the relationship between the frequency of a sound, the number of vibrations per second, and the perceived pitch of the sound when we listen to it is non-linear, in fact it is logarithmic. In standard tuning, the note A below middle-C has a frequency of 220 hertz (Hz), or 220 vibrations per second. The next higher A on the piano keyboard has a frequency of 440 Hz, 220 Hz higher. The next higher A has a frequency of 880 Hz, not 220 Hz higher, but 440 Hz higher. The constant in the relationship between different A notes is that each is double the frequency of the one below. The A below middle-C has frequency 220 Hz, the next one up is double that, 440 Hz, the next one is double again, 880 Hz, and so on. This multiplication of frequencies is what is meant by a "logarithmic" relationship.

Notes on pianos and guitars are generated by strings vibrating at specific frequencies.

Notes which are exactly double the frequency of other notes are given the same letters as names because to our ears they sound exceptionally harmonious when played together. In fact, in some sense they sound like almost the same note, even though the physical frequencies are different. There's a reason for this which we'll get to later, but for now just know that if you play a 440 Hz A and a 880 Hz A together, they sound nice. This doubling of frequency constitutes a certain pitch interval to our auditory system (our ears and brain); this interval is named an octave.

If you ask someone, even with no musical training, to listen to the two notes A at 220 Hz and A at 440 Hz one after the other, and then to sing a note the same pitch distance above the second as the second is above the first, they will sing the A at 880 Hz. If you play these three notes in sequence, they sound like they are going up in pitch in evenly spaced steps. The frequency 660 Hz doesn't even get a look in, and if you try playing that to people as the third note they will say it's wrong. So it is definitely the ratio between physical frequencies that determines our perception of musical pitch, not the difference.

Ratios other than doubling can sound good too. If you play 440 Hz and 660 Hz together, they sound melodious and pleasant. The same thing if you play 220 Hz and 330 Hz. The pitch intervals between these two pairs of frequencies sound like the same distance in perceptual pitch, and again it's because they have the same ratio - the higher note is 1.5 times the frequency of the lower, which we can write as the pairs of frequencies being in the ratio 2:3. After the octave, which is a frequency ratio of 1:2, this is the next simplest ratio writable using small integers. The melodious pitch interval so generated is used very commonly in music, and is called a perfect fifth (for reasons which are not yet obvious but will hopefully become so). If you start at middle-C, the note a perfect fifth above it is G, and if you play middle-C and the G above it together, they sound harmonious and pleasant together.

The next simplest frequency ratio is 3:4. If we start at 440 Hz again, the resulting frequency is 586.66 Hz. This ratio, and its corresponding pitch interval, is named a perfect fourth, and also appears in our musical system. If you start at middle-C, the note a perfect fourth above it is F, and similarly to the perfect fifth, if you play middle-C and the F above it together, they sound harmonious.

The next simplest frequency ratio is 4:5. If we start at 440 Hz again, the resulting frequency is 550 Hz. This ratio, and its corresponding pitch interval, is named a major third, and also appears in our musical system. If you start at middle-C, the note a major third above it is E, and similarly again, if you play middle-C and the E above it together, they sound harmonious.

Rather than continuing on in this way generating harmonious sounds forever, these pitch intervals start to get less harmonious sounding to our auditory systems as the ratios start involving larger and larger integers. For this reason, much of the music of the Western musical culture is built most strongly around the above-mentioned pitch intervals: the octave, perfect fifth, perfect fourth, and major third. Other intervals are used for colour and interest, but less often.

Going back to the octave, if we just keep doubling a frequency multiple times, we generate new notes pitched higher and higher, but always sounding very similar to our ears. These are the multiple versions of the named notes, for example middle-C, the C above middle-C, the next C above that, and so on.

We can do the same thing for the perfect fifth. If we start at middle-C and find the note with a frequency 1.5 times, it turns out to be G (as mentioned above). But what is a perfect fifth above G? Its frequency will by 1.5×1.5 = 2.25 times that of middle-C. If you do this calculation, you discover that it is the note D, just above the C above middle-C. You can keep going, multiplying the frequency by 1.5 each time and producing a new note which is harmonious with the one immediately below (being separated from it by a perfect fifth). The sequence of notes so generated turns out to be: C-G-D-A-E-B-G♭-D♭-A♭-E♭-B♭-F-C; where the ♭ symbol indicates "flat", so "G♭" is G-flat.^[2]

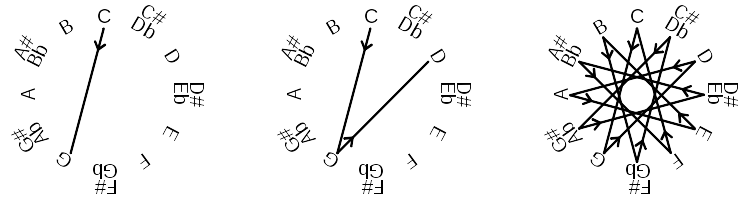The 12 notes in an octave arranged in a circle, showing construction of what notes are reached by going up intervals of a perfect fifth successively. Creative Commons Attribution image by Wikimedia Commons user Tcolgan001 from Wikimedia Commons.

Notice that this sequence of notes exactly matches the named notes on a piano keyboard, except for being mixed up in ordering. The white keys in an octave in order up the keyboard are C-D-E-F-G-A-B-C, and the intermediate black keys are, in order, D♭-E♭-G♭-A♭-B♭ (or equivalently written as sharps C♯-D♯-F♯-G♯-A♯). And, more importantly, notice that it cycles around to C again. This is because after 12 intervals of a perfect fifth, we have multiplied the frequency of our starting note by 1.5¹² = 129.746... This number is close to 128, which is equal to 2⁷. So after starting at C and going up by a major fifth 12 times, we come to a note which is approximately 7 octaves above the C where we started.

This mathematical coincidence is close enough that our ears can adjust for it if we do a clever little trick. The octave is the most fundamental interval of all, so we don't mess with that. Instead, we redefine the ratio that is used to make the perfect fifth. That ratio is ideally 1.5 (which is the twelfth root of 129.746..). But what if we use the fact that 1.5¹² = 129.746.. ≈ 128 = 2⁷ take the twelfth root of 128 instead?

The twelfth root of 128 is 1.4983... This happens to be so close to 1.5 that when we play notes with the frequency ratio 1.4983.., they sound to our ears almost exactly as harmonious as notes separated by a frequency ratio of exactly 1.5. Some highly trained musicians may be able to tell the difference, but most people can't. So in modern musical tuning, this is typically exactly what's done. A piano tuner will not tune your G key to be exactly 1.5 times the frequency of your middle-C key, they will tune it to be 1.4983.. times the frequency of middle-C (unless you instruct them otherwise^[3]). Similarly, all the other intervals on your piano keyboard are typically tuned with frequency ratios based on twelfth roots of 2. This sort of tuning is called equal temperament, and the results are shown in the table.

Note	Interval	Exact ratio	Approx. ratio	Approximates this interval
C	Unison	2^0/12 = 1	1.0000	1/1 = 1
C♯	Minor second	2^1/12	1.0595	16/15 = 1.066..
D	Major second	2^2/12	1.1224	9/8 = 1.125
D♯	Minor third	2^3/12	1.1892	6/5 = 1.2
E	Major Third	2^4/12	1.2599	5/4 = 1.25
F	Perfect fourth	2^5/12	1.3348	4/3 = 1.333..
F♯	Augmented fourth	2^6/12	1.4142	7/5 = 1.4
G	Perfect fifth	2^7/12	1.4983	3/2 = 1.5
G♯	Minor sixth	2^8/12	1.5874	8/5 = 1.6
A	Major sixth	2^9/12	1.6818	5/3 = 1.666..
A♯	Minor seventh	2^10/12	1.7818	16/9 = 1.777..
B	Major seventh	2^11/12	1.8877	15/8 = 1.875
C	Octave	2^12/12 = 2	2.0000	2/1 = 2

You can see that the perfect fourth (ratio 3:4) and major third (ratio 4:5) are also quite well approximated by this tuning system, as are several other ratios with small integers. And... here we have the thing I craved all those years ago when I didn't understand any of this: A set of notes where the intervals between them are all evenly spaced in frequency ratio! Indeed, if you play all the piano keys in an octave, the white ones and the black ones, you end up with a 12-note scale with mathematically (logarithmically) equally spaced pitch intervals.

The question is: Does such a musical scale actually sound any good? This 12-note scale is called a chromatic scale and is in fact used in various pieces of music. The interesting thing is that chromatic pieces of music are often described as "dissonant" or "inharmonious", and the chromatic scale is often deliberately used to produce works or passages of music that evoke negative feelings such as discomfort or disgust. In other words, this is not a scale to use if you want your music to sound melodious and tuneful.

Rather than use all of the available notes equally, most music places much more emphasis and repetition on some specific subset of the 12 chromatic notes. Such a subset is termed a scale. It turns out that a subset made up of seven notes within an octave (with the octave itself making up the eighth note in sequence - thus the name "octave") sounds pretty good when music is written using just those notes. This is (at least partly) because we have gotten rid of some of the higher integer frequency ratios, which sound less harmonious than the lower integer ratios. The particular notes we use in such a scale are the ones corresponding to the most harmonious intervals - the perfect fifth, fourth, major third, and a couple of others. And removing the least harmonious intervals results in the remaining notes being unevenly spaced - producing the interval pattern as we climb the notes of the scale: tone-tone-semitone-tone-tone-tone-semitone. This is the origin of the uneven spacing that so vexed me as a younger person.

You can pick different subsets of the 12 chromatic notes to base your music around. A set of the 5 most harmonious intervals produces the pentatonic scale, which is used a lot in Western folk music and in East Asian music, giving them their distinctive musical flavours.

The uneven spacings of the scales provide "anchor points" for your auditory system while listening to the music. Music written on just the white keys of a piano (C-D-E-F-G-A-B-C), for example, often tends to use the note C a lot. You can tell it's the note C (even without musical training or knowledge of what the note is named - virtually everyone familiar with Western music just by listening to the radio has this ability) just by listening to the pattern of intervals between the notes that appear in the music. Most people don't do this consciously, but if you hear a piece of music written in this way (i.e. in what is called the C-major scale), you start to feel a sort of auditory desire to hear the note C in the music, and every time the music delivers a C, you feel a sense of pleasure and satisfaction. Composers know this, and they often write songs or pieces of music which tickle your musical sense by flirting with that C note throughout the piece, and then resolve at the end of the song by delivering a resounding C note to finish the song off - which gives you the listener a sense of completion and satisfaction.

Everything in the previous paragraph can be transposed to a different scale which starts on a different piano key, but then follows the same pattern of tone-tone-semitone-tone-tone-tone-semitone. If you start on G instead of C, you end up with the notes G-A-B-C-D-E-F♯-G. Notice there is an F♯ in there, to preserve the pattern of tones and semitones. If you play music written using these notes, listeners tend to fixate on the note G, and expect G to appear a lot, and composers will often tend to complete their songs on a G note. This scale is called the G-major scale.

You may have noticed that within the 12 notes of the chromatic scale your can extract an evenly spaced subset by taking six notes instead of seven (or five): C-D-E-F♯-G♯-A♯-C. A six-note scale is called a hexatonic scale, and in particular this one is called the whole tone scale, and indeed it is occasionally used in music. A problem with this scale is that there is no anchor point. There is no pattern of tones and semitones to tell the listener where they are on the scale, so it feels like there is no dominant note. It's not like C-major, where the listener expects the C, and the composer can use this expectation to set up tension and resolution. The whole tone scale cannot be used that way - it feels slippery and indistinct. This can be used for certain musical feelings and effects, but it doesn't mesh well with the standards of music we are accustomed to, which is why it is seldom used.

So, in what has turned out to be a much, much longer annotation than I expected to write today, there in a nutshell is why the white keys on a piano are unevenly spaced in terms of mathematical frequency ratios. There is much, much more I could say about musical scales and tunings - in particular minor scales, and all the mathematical complexities of just intonation tuning^[3] - and also about the musical topics of melody, rhythm, timbre, harmonics, and so on, but it's time to wrap this one up for today.

Oh, and it's called a "perfect fifth" because this interval gets you to the fifth note of the major scale. If you start at C, the fifth note of the C-major scale is (C-D-E-F-G) G. That's why the interval from C to G is called a fifth. Similarly C to F is a fourth, and C to E is a third. This caused me no end of confusion some years ago when I was first trying to understand this stuff, because as a mathematician my instinct was that an interval named a "third" had to be bigger than an interval named a "fifth" (because 1/3 is bigger than 1/5). It would help a lot if musicians called these intervals "major three", "major four", and "perfect five" instead of "major third", "major fourth", and "perfect fifth", but I suspect getting them all to change is a losing battle...

(EDIT: Several people wrote to say that the names are not fractions (one, half, third, fourth, fifth,...) but ordinals (first, second, third, fourth, fifth,...). Which actually makes a lot of sense - but unfortunately nobody ever explained it to me that way.)

Me playing the drums with the School of Rock band I participated in last year. Thankfully, for drums I don't actually need to know any of this scale stuff!

[1] Interestingly, about a year after I started formal lessons in drumming - the first real music lessons I've ever had. Yep, you don't need to know squat about music theory to learn to play the drums!

True story: When I began learning drums, my teacher asked me which drummers I liked. I said: Rob Hirst (Midnight Oil), Jon Farris (INXS), Mick Fleetwood (Fleetwood Mac), Ringo Starr (The Beatles), Dominic Howard (Muse), and Animal (Dr Teeth and the Electric Mayhem). My teacher said, "Oh, well, all drummers like Animal".

[2] This sequence is known as the circle of fifths, and forms an important part of music theory, which I don't have time to go into further here.

[3] Very briefly: You don't have to tune your piano or other instrument using the equi-spaced system described here which approximates the intervals of perfect fifths, fourths, major thirds, and so on. Instead, you can tune your G exactly 1.5 times the frequency of your C, and so on. This messes up your circle of fifths, but can work within a small pitch range, for a specific scale. It prevents you easily transposing your music to a new scale, as the intervals will all mismatch, but for any given scale it works fine. This sort of tuning is called just intonation, in contrast to the equal temperament tuning described in the main body text above.