Irregular Webcomic! #3374

Decimals are a way of writing fractional numbers using the same base-ten digit system we use for writing whole numbers. In the whole number system, the rightmost digit represents the number of ones (or "units") in our number. The next digit to the left indicates the number of tens, the next digit left indicates the number of hundreds, the next digit left the number of thousands, and so on. So the number we write down as 358 is made up of eight ones, and five tens, and three hundreds. If you do the multiplications and additions: 8×1 + 5×10 + 3×100, the answer comes out to three hundred and fifty eight.

Each of the amounts one, ten, hundred, thousand, and so on, is a power of ten, increasing by one power for each step to the left. One is ten to the power zero; ten is ten to the power one; a hundred is ten to the power two; a thousand is ten to the power three; and so on. The pattern should hopefully be clear: the power for the rightmost digit is zero, and it increases by one for each digit you step to the left.

You can also extend the pattern to the right. To mark the starting point, we put a decimal point^[1] immediately to the right of the "ones" digit. The first digit to the right of the decimal point indicates how many [ten to the power minus one]s there are in a number. Ten to the power minus one happens to be the fraction one tenth. Ten to the power minus two is the fraction one hundredth. Ten to the power minus three is the fraction one thousandth. And so on.

So for example the number we write down as 0.25 is made up of zero ones, and two tenths, and five hundredths. If you do the multiplications and addition: 2×(1/10) + 5×(1/100), the answer comes out to twenty-five hundredths, which we can write as 25/100, which represents the same (fractional) number as one quarter, which we can also write as 1/4.

An interesting asymmetry with this way of writing down numbers as strings of decimal digits is that as you go left, the digits represent numbers that keep getting bigger and bigger. There's no limit to how big a number you can write down. At least in principle - eventually you'll run out of paper and ink and enough space in the universe to fit it in. But ignoring those limits, no matter how big a number I write down in standard decimal notation, you can always make a bigger number just by adding an extra digit to the left side. The magnitude of the numbers you can represent this way is unbounded.

On the other hand, the digits to the right of the decimal point represent numbers that keep getting smaller and smaller. You can keep adding more digits to the right side, and the number you are representing gets bigger, but there's a limit or bound to how big it can get. If your number you are writing down begins "4.36" and then you add more digits to the right side (e.g. "4.3627491...") the number you are representing gets bigger than 4.36, but it can never get bigger than 4.37, no matter how many extra digits you add.

This runs us into the concept of infinite limits and how we represent certain numbers using decimal notation. The fraction one-quarter can be written as 0.25, because a quarter is equal to twenty-five hundredths (i.e. twenty-five divided by a hundred), and hundredths are a power of ten. The fraction one-third, however, is not equal to any whole number divided by any power of ten. If you divide by ten, the closest you can get is three divided by ten. If you divide by a hundred, the closest you can get is thirty-three divided by a hundred. If you divide a whole number by a thousand, the closest you can get to a third is three hundred and thirty-three divided by a thousand. And so on, getting ever closer to exactly a third at each step, but never quite reaching it.

This is reflected in the decimal representation of one-third, which looks like this: 0.3333..., where the "..." indicates that the pattern of every digit being a "3" continues on indefinitely, without ever coming to an end. A decimal string of digits consisting of "0." followed by any given finite number of "3" digits does not represent the number one-third, as you can always get closer to one-third by adding more "3"s on to the right side. However if you let the number of "3"s on the right side extend forever, never coming to an end, then a curious thing happens. Such an infinite string of decimal digits represents what is called the limit to which all the ever longer possible finite strings of digits can get ever closer to, but never exceed.

A string consisting of "0." followed by a finite number of "3"s represents a number which can get as close as you like to one-third, just by having enough "3"s. Want it to be within one-hundredth of one-third? Here you go: 0.33. Want it closer, to within a thousandth? Easy: 0.333. To within one-billionth? Trivial: 0.333333333. You can choose an increment as small as you like, and I can write down "0." followed by some finite number of "3"s which represents a decimal number that is within your chosen increment of one-third. But: I can never write down such a string which exceeds one-third. These two properties together define that the limit of ever-longer finite strings of this form is equal to one-third (even if any given finite string is a little less than one-third). And the infinite string consisting of "0." followed by an endless number of "3"s that goes on forever represents that limiting number - in this case one-third exactly.

Fortunately we have a shorthand way of writing down infinitely repeating decimal representations of numbers. Instead of writing down an infinite number of "3"s (which we can't do), we can just write "0.333...", where the "..." part indicates the established pattern of digits continues forever. In fact, we have a few different ways of writing down the same decimal representation, using dots or bars over the digits, which I can't show in plain text but are shown in the figure below:

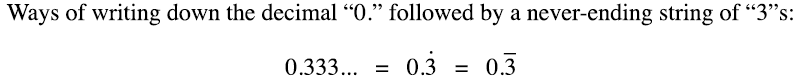
One-third is not the only fraction to have such an infinitely long decimal representation. In fact most fractions are like this. It's only fractions which are equivalent to a whole number divided by a power of ten that can be written as a finite decimal like 0.25 (twenty-five hundredths, which equals one-quarter), and that's actually a very restricted subset.

The number one-sixth is written as a decimal like this: 0.1666..., where the "6"s keep going on forever. The number one-seventh is interesting; as a decimal it looks like this: 0.142857142857..., where the pattern of six digits "142857" repeats in the same cycle forever. One-ninth written as a decimal looks like this: 0.111.... One-eleventh as a decimal looks like this: 0.090909... where the "09" repeats forever.

These never-ending decimal representations can be manipulated using the basic rules of arithmetic like other numerical representations, with the small twist that you need to remember they go on forever. To multiply a decimal representation, you normally start at the rightmost digit, but these never-ending ones don't have a rightmost digit. So you need to apply a bit of logic to figure out what happens.

For example, let's multiply the decimal representation of the number one-sixth by two. One-sixth is written as 0.1666.... Rather than start multiplying at the rightmost digit (which we can't do), let's figure out what the first digit after the decimal point of our answer must be. The corresponding digit of one-sixth is "1", which gives "2" when multiplied by two. But that's not the full story, because the second digit of one-sixth is a "6", which gives "12" when multiplied by two, and we need to carry the "1" across to the left and add it to the "2" we generate there, giving us "3" in the first digit, and leaving "2" in the second digit. We never carry more than one place, so the "3" in the first place after the decimal point can't change any further, and that is the first digit of our answer. But similarly, the "2" we've generated for the second digit is not the final answer for that digit, because the third digit of one-sixth is also a "6", again giving "12" when multiplied by two, meaning we carry the "1" across again. This makes the second digit of our answer "3". Similarly, the third digit of our answer is also "3" after carrying a "1" across from the fourth digit, and so on, and the same pattern repeats at every digit, forever. This pattern never ends, as the decimal representation of one-sixth never ends. So our answer ends up being a decimal point followed by a never-ending series of the digit "3", in other words 0.333.... And we've seen this decimal string before - it is the decimal representation of the number one-third! So one-sixth multiplied by two equals one-third.

Of course, we knew that answer already because one-sixth can also be written as a fraction like this: 1/6, and we can multiply it by two using fractional notation like so: 1/6 × 2 = 2/6 = 1/3, where we have cancelled the fraction down in the last step, resulting in the fractional notation representation of the number one-third. That you can do the same operation in decimal notation and reach the same answer (one-sixth times two equals one-third) is reassuring!

You can also multiply, for example, one-third by two. In decimal notation, one-third is 0.333..., and there is no tricky carrying this time. You can just multiply each digit "3" in the never-ending string by two to give a "6", and build the never-ending string 0.666..., which is the decimal representation of the number two-thirds. And since we know one-third times two equals two-thirds, that all works fine.

We can also multiply one-third by three. In decimal notation, one-third is 0.333..., and again there is no tricky carrying. You can just multiply each digit "3" in the never-ending string by three to give a "9", and build the never-ending string 0.999..., which is a decimal representation of the number three-thirds. And since we know one-third times three equals three-thirds, that all works fine.

Except three-thirds is just another way of saying the number one. One-third times three equals one. And we usually write the number one as 1, or if we want to put something after a decimal point, as 1.0.

What's going on here? Have we done something wrong? The answer, which might seem astonishing at first, is that the decimal string written as 0.999... represents the same number as is represented by the decimal string 1.0, namely the number one. It is a simple fact of mathematical notation that you can write a representation of the same number in many different ways. We've already seen that above. You can write down the number one-third as either 1/3 or 0.333..., or even as 2/6. Each of these three notations represents exactly the same number.

Similarly, you can write down the number one as 1 or 1.0 or 1/1 or 2/2 or 2-1 or (-1)² or -i² or -e^iπ or any one of a (quite literally) infinite number of other ways. Each of these arrangements of digits and symbols on a page or a screen represents the number we know as one. And here for the first time I am stressing the word represents, even though I have been using it a lot already in the text above. The digit "1" is not the number one - it is a symbol which represents the abstract concept that is the number one. Similarly, the symbols "-e^iπ" are not the number one - they are a group of symbols which represent the abstract concept that is the number one. And similarly again, the decimal string "0.999..." is not the number one - it is a group of symbols which represent the abstract concept that is the number one.

However, there is a substantial amount of disbelief (for want of a better word) about what I have stated in the last sentence of the previous paragraph. Many people, including many with a good mathematical education, find it difficult to believe that the decimal string 0.999... (where it is understood that the "9"s never end) represents the number one. Firstly, it doesn't look like it should be equal to one. It starts with "0.9" and we are trained to recognise that strings which start like that represent numbers which are less than one. Secondly, there's already a well-known string of digits that represents the number one, namely "1". We also have this gut feeling that there should only be one way to write down any given number.

Addressing the second point first, our feeling that there should only be one way to write down any given number is simply wrong. You can also write down the number one, as we've already seen above, as 1 or 1.0 or 1/1 or 2/2 or 2-1 or (-1)² or -i² or -e^iπ. The simple fact is that there are lots of ways of writing down a bunch of symbols in our mathematical notation to represent the same number. 0.999... is simply another way of writing down the number one.

The first point is a bit more difficult to counter. We have this ingrained feeling that any decimal string which starts with "0.9" must - surely must- be less than one. The most basic counter to this is simply to point out that this ingrained feeling is actually wrong. No matter what we may have been taught at school about mathematics, or what we feel deep in our gut to be right, it is actually wrong that the string 0.999... represents a number that is less than one.

A more logically based argument goes like this: Okay, if the number represented by the never-ending string of "9"s which we write in shorthand as 0.999... is less than one, then how much less than one is it?

Specify some tiny fractional number. One hundredth? No, it's closer to one than that. A millionth? Nope, it's closer to one than that. A billion billion billion billionth? No, the number represented by 0.999... is closer to one than that. It doesn't matter what tiny fractional number you name, the number represented by 0.999... is closer to one than that, because the "9"s go on forever without end, you can always just travel far enough to the right to reach the point where your fractional number is bigger than the difference between the number represented by 0.999... and one. The only (non-negative) number for which the number represented by 0.999... isn't closer than that to one, is zero. Which is really just saying that the difference between the number represented by 0.999... and one is zero. In other words, the number represented by 0.999... is one.

There's nothing wrong with the fact that the number one can be written down as a decimal either as 1.0 or 0.999.... It's similar to how there's nothing wrong with the fact that the idea of a cat can written down as the words "a cat", but also as the words "un gatto" (in Italian). 0.999... and 1 are different "numbers" in the same sense that "a cat" and "un gatto" are different animals. The phrase "a cat" is not an actual cat, and neither is "un gatto"; they are both just ways of writing down a representation that we understand as referring to some animal of a particular type. In the same way, 0.999... and 1 are not actual numbers; they are just ways of writing down a representation of some number. This sort of semantic distinction is known as the map-territory relation.

Thus we get to the point of the comic above. Indeed, "0.999..." is not one (or "une" in French). But then neither is "1". Both of these sets of symbols are just ways that we can write down a representation of the abstract object that is the number one.

Now, despite everything I've said above, there will almost certainly be readers out there who don't believe what I've said about the decimal string "0.999..." representing a number which is equal to one. For some reason this is a notoriously difficult thing to convince people of, even though it is demonstrably true with nothing more complicated than basic arithmetic. People really cling to the idea that two numerical representations which look so different must actually represent different numbers. I'm not going to spend further effort here trying to convince anyone who is not yet convinced, because it is probably a losing proposition at this point.

But I will say that this particular case is a fascinating study in how people can believe things which are contrary to both logic and fact, simply because they have been taught one thing and then try to apply it too generally. It is a classic case where many people's common sense tells them something which is patently untrue, resulting in them disbelieving the truth. And if you want to spend more time reading and pondering about it, the talk pages (and "argument" pages) on Wikipedia's article for 0.999... are full of more or less interesting comments.

The article itself has a particularly revealing comment, quoted from mathematics educator David Tall (co-author of several books with well-known mathematics populariser Ian Stewart):

Of the elementary proofs, multiplying 0.333... = 1/3 by 3 is apparently a successful strategy for convincing reluctant students that 0.999... = 1. Still, when confronted with the conflict between their belief of the first equation and their disbelief of the second, some students either begin to disbelieve the first equation or simply become frustrated.

Paraphrasing: When confronted with a true statement B which their common sense (incorrectly) tells them is false, and then shown a proof beginning with a much more obviously true statement A which leads logically to statement B, some people begin to question the truth of the statement A, rather than accepting the truth of statement B. It really is that hard to fight against a person's in-built sense of "common sense". Psychologically, it's a very difficult thing to do.

So beginning with basic arithmetic we arrive at a fascinating observation about people and human psychology. It's interesting where things can lead you....

[1] The decimal point is marked by a dot in most English speaking countries, and by a comma in continental Europe.