1 {photo of Canterbury College in Christchurch, where Ernest Rutherford studied}
1 Caption: Probing the atom

A rock, being pushed.

By the mid 19th century, scientists experimenting with static electricity had determined that matter contained some substance that carried an electric charge.

What is an electric charge, exactly? That's a difficult question to answer on the most fundamental level, but functionally an electric charge is something that feels a force when in the presence of another electric charge^[1]. It might be pushed away or pulled towards that other charge. This property, plus the fact that electric charges can be made to move around, results in all of the various phenomena we associate with electricity.

So, electric charge exists. How does it relate to matter and, specifically, how is it related to atoms? The first attempt to answer this was by British scientist J. J. Thomson, the man who discovered the electron in 1897. He realised that electric charge was carried by particles that were contained within atoms. Atoms were usually electrically neutral, he said. That is, they contained the same amount of positive electric charge as negative electric charge. When you rub two suitable materials together, electrons (which we discussed previously) get pulled out of the atoms of one material and deposited on to the other material. This explanation by itself is enough to explain the known properties of electricity at the time.

Plum pudding.

The main question was: how exactly are the electrons and... other bits of an atom arranged? In 1904, Thomson proposed that atoms were kind of like a plum pudding. A big lump of atomic pudding goodness, with little electrons sprinkled throughout like plums (or currants^[2] if you prefer). The pudding part of the atom had a positive charge equal in size to the total negative charge on the plums/electrons. Rubbing materials together plucked some of the electrons out of the atomic puddings in one material and deposited them on the other material.

Thomson's plum pudding model of the atom lasted for five years. One of his own former students directed the experiment that disproved it in 1909. Ernest Rutherford supervised Hans Geiger (inventor of the Geiger counter) and Ernest Marsden in the experiment, in which they fired positively charged helium atoms (i.e. with the electrons stripped off) at a thin sheet of gold foil. It was known at the time that the helium atoms passed through the gold foil, indicating that atoms were diffuse in some sense. A sheet of atoms was not like a brick wall that stopped anything passing through; it was more like a sieve, which let objects as small as other atoms pass straight through. A bit like bullets being fired at a wall made of plum puddings, in fact.

Gold foil. (actually, aluminium foil, coloured gold...)

For this experiment, Geiger and Marsden had built a special detector which could be swivelled accurately around the gold foil to measure the angle at which the helium atoms emerged from the foil. Although the atoms passed pretty much straight through, they expected there to be some very small deflections. By building up a statistical sample of the deflection angles, they hoped to map out how the positive and negative charges were distributed inside the atoms of gold in the foil. Basically, if a helium atom passed through a region of the foil where these charges balanced out, it would not be deflected at all. On the other hand, if it happened to pass through a region where one side was a bit more negative and the other side a bit more positively charged, this would cause a slight deflection. By analysing the amount of any deflections, and how many deflections occurred, Geiger and Marsden would be able to map out how the charge was arranged in the gold foil.

To their surprise, they found that there was almost no deflection at all. Pretty much all of the charged helium atoms passed through completely unscathed, with a deflection angle of zero degrees. A very few helium atoms were deflected by small angles.

Just for completeness, they swivelled their detector all the way around the gold foil, and then a most astonishing thing happened. Some of the charged helium atoms had been deflected by really large angles, 90 degrees or more. What's more, some of them had bounced off the foil, almost straight back where they came from! This was completely unexpected. In Rutherford's own words:

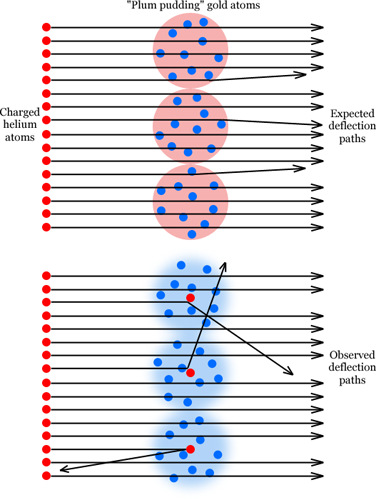Top: Charged helium atoms fired at gold foil made of plum pudding atoms, with expected deflection paths. Bottom: Observed results of the experiment. Positive electric charges are red, negative charges are blue.

It was quite the most incredible event that has ever happened to me in my life. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you.

What was going on here? It took Rutherford and his colleagues two years to formulate and publish their explanation, in 1911. The only way to explain what they had observed was to conclude that the positively charged part of the gold atoms was extremely small, in fact much smaller than the size of the atoms themselves. Doing the calculations, the positive charge in a gold atom had to be about 1/4000 of the size of the atom overall. This way, nearly all of the charged helium atoms hitting the gold foil would simply pass through empty space, but occasionally one would come close to hitting this nucleus and be deflected by a substantial angle, and sometimes one would hit it almost dead on and be bounced straight back to where it came from.

Rutherford's model of the atom consisted of a tiny, positively charged nucleus, which contained all of the positive charge of the atom. The electrons had to be further away, not embedded within the nucleus like Thomson's plum pudding. But remember that positive charges (like the nucleus) and negative charges (like the electrons) are attracted to one another. How could they be held apart? To explain this, Rutherford took inspiration from another physical system in which objects that are mutually attracted to one another are held at a great distance in a stable arrangement: planets in orbit around the sun. In Rutherford's model of the atom, the electrons were like planets, orbiting at a relatively large distance around a small nucleus, and held in this arrangement by the attraction of their electric charges.

This result implied that the electrons were an important part of what makes up an atom, not merely unnecessary adornments like plums in a pudding. In Thomson's model, the pudding was the atom, and (to mix metaphors) the electrons were like fleas that just hitched along for the ride. In Rutherford's model, the electrons were the outer layers of the atom. If you stripped the electrons away, you wouldn't have a plumless pudding atom left over, you'd have something much, much smaller than an atom. The distinction may sound subtle, but Rutherford's result was the first really strong hint that atoms were in fact not indivisible balls of matter (that attracted the mysterious electrons). Atoms were made of smaller particles.

This was a closer model to reality than the plum pudding atom but, as it turned out, Rutherford's model lasted an even shorter time than Thomson's five years. The problem with Rutherford's model was that it required the charged electrons to move in circular (or elliptical) orbits around the nucleus. In 1897, Joseph Larmor had shown, using Maxwell's equations of electromagnetism (which I've discussed previously - you may want to refresh your memory), that an electric charge moving in a circle will emit electromagnetic radiation (i.e. light, or radio waves, or x-rays, etc.) So the electrons in Rutherford's model should be constantly emitting radiation. And when they emit radiation, they lose energy, which means they can't stay in the same orbit - they should spiral in towards the nucleus^[3].

In other words, if atoms were really like Rutherford's model, then they should all spontaneously collapse in a flash of radiation. They obviously don't do this, so something was wrong.

Visible spectrum of hydrogen. Adapted from public domain image from Wikimedia Commons.

The secret to unravelling this problem was in an apparently unrelated piece of work done 23 years earlier by Johannes Rydberg. Rydberg was interested in the emission spectrum of hydrogen. When you give a sample of hydrogen lots of spare energy by heating it up or passing an electric current rhough it, it starts to glow. But it doesn't glow with a white light made up of all the colours of the spectrum. It glows with an extremely sparse spectrum of colours, which includes just 4 distinct and separate colours of light. If you split up the light from glowing hydrogen using a prism, you don't get a continuous rainbow, you get 4 very sharp and distinct lines of colour. There's a red one, a bluey-green one, a blue one, and a violet one. What Rydberg did was to come up with a mathematical formula that related the wavelengths of these hydrogen emission lines.

Rydberg made his formula work for the non-visible lines of the hydrogen spectrum as well - those in the ultraviolet and infrared parts of the spectrum. His formula looks like this:

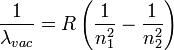
Some red, hot objects.

λ_vac is the wavelength of a hydrogen spectral line measured in a vacuum (a small adustment is needed if you measure it in air). n₁ and n₂ are positive integers, whole numbers from 1, 2, 3, upwards. And R is a constant number, now called the Rydberg constant. If you pick any numbers you like for n₁ and n₂, plug them in, then the wavelength you get will be one of the wavelengths of radiation emitted by hydrogen. Furthermore, every wavelength of radiation that hydrogen emits can be matched up to this formula for some positive whole numbers n₁ and n₂. Rydberg's formula worked perfectly.

Rydberg published his result in 1888. It was a triumph of experimental physics. The only trouble was that nobody had any idea why it worked.

In 1912, a year after Rutherford published his model of the atom, the Danish physicist Neils Bohr joined his research team in Manchester. Bohr was disturbed by both the theoretical problem in Rutherford's atomic model, and the lack of any physical explanation for Rydberg's formula. He addressed both of these in a single brilliant insight, by using a third piece of recent physics.

In order to explain the observed spectrum of light emitted by a hot object (a red hot piece of iron, the sun, a white hot material, etc.), Max Planck had formulated a theory in 1901, in which electromagnetic radiation is emitted not continuously, but is quantised into separate, discrete "packets" of energy. The details are too much to go into now, but his main result was that when an electric charge oscillates in a hot object, it doesn't lose energy continuously, but rather in discrete jumps. Furthermore the jumps in energy are related to the wavelength of the light that ends up being emitted, by the simple formula:

E = hν

Jumping between energy levels.

E is the amount of energy lost by the oscillating charge, ν is the frequency of the light emitted (equal to the speed of light divided by the wavelength), and h is a constant number, now known as Planck's constant. By using this relation, Planck solved the problems with understanding the radiation emission spectrum of hot objects.

Bohr realised that Planck's treatment of hot oscillating charges could also be applied to the movement of electrons in an atom. Bohr proposed that electrons orbiting a nucleus could also not lose energy continuousy (as predicted by Maxwell's equations), but only in discrete jumps, with energy related to the wavelength of light by Planck's formula. Certain fixed orbits of the electrons were therefore stable over long periods of time, and the electrons could only "jump" between the orbits by gaining or losing a fixed amount of energy. The energies of the orbits were such that the angular momentum of electrons circling the nucleus were whole number multiples of Planck's constant divided by 2π (that factor comes in because we're talking about angular momentum instead of energy):

(angular momentum) L = n / 2π; where n is a whole number.

By making these assumptions, Bohr showed that the radiation spectrum emitted by a hydrogen atom could be explained as the electrons jumping between orbits of differing energies. This matched Rydberg's formula, with n₁ and n₂ being precisely equal to the whole number multiples n of the two different orbits which the electron jumps from, and jumps to. Furthermore, this model allowed Bohr to calculate the value that the Rydberg constant R shoud have, in terms of the Planck constant, the mass of the electron, the charge of the electron, the speed of light, and the permittivity of free space constant from Maxwell's equations. And when Bohr plugged in all these numbers, he got the same value for the Rydberg constant that Rydberg had measured experimentally. How good is that?

Humboldt University, Berlin. Where Max Planck taught physics.

Bohr's model of the atom was published in 1913 and was an immediate triumph. It solved two outstanding problems of physics (Rydberg's formula and Rutherford's model), by using a brand new idea developed to explain a completely different problem (Planck's quantised black body radiation theory). Besides providing the clearest understanding yet devised of how an atom actually works, it also provided support for Planck's ideas about quantisation of energy.

Bohr's model has since been superseded, but it still survives as the first mathematically rigorous and useful approximation taught to physics students today. (Similar to how students are first taught Newton's laws of motion, rather than thrown straight into Einstein's special and general relativity.) Furthermore, in historical context, Bohr's model was a crucial stepping stone to the newly developing theory of quantum mechanics that would change the world in the next few decades.

In 1913, less than a hundred years ago, we had our first glimpse of understanding of how atoms really work.

Addendum: I mentioned in an earlier annotation that electricity is the answer to two puzzling historical questions about the properties of atoms and elements. We're getting closer, but we still need a little bit more work to answer those questions:

1. Why are the atomic weights of many of the elements so tantalisingly close to whole number multiples of the weight of a hydrogen atom? And why are a few of them not close at all?
2. Why are the chemical properties of the elements related to the weights of their atoms?

Stay tuned.

---

[1] This may sound like a bit of a cop-out explanation. I know it never satisfied me when I was studying physics at high school. It seems kind of hand-wavey and not really getting down into the guts of what electric charge really is, if you see what I mean. But later on I realised that the only relatively simple explanation of what mass is, is: something that feels a force when in the presence of another mass. (That force being gravity, rather than electric force.) Yet I'm perfectly comfortable with mass; I feel like I really, truly understand mass on an instinctive level. That "understanding" is really just familiarity. We interact with mass every single minute of our lives. We know how mass behaves under gravity, without having to think about it. It's so familiar that we just feel, deep down, like we know what it is. We don't have the same everyday familiarity with electric charge and its behaviour. That's why electric charge feels so abstract, even though, fundamentally, it's a very similar physical phenomenon to mass. (There are some very important differences hidden way under the covers, but for the purposes of today's discussion they don't really come into it.)

[2] Ha, currants. Get it?

[3] In the same way that satellites that lose energy by dragging through the topmost parts of Earth's atmosphere eventually spiral down and crash into Earth. (In an even closer analogy, satellites also lose energy by radiating gravitational waves—"waves of gravity"—which are somewhat similar to electromagnetic radiation being "waves of electric field". However, the loss of energy from a satellite by gravitational radiation is too small to be measured, and vastly overwhelmed by the loss due to upper atmospheric friction.)